Introduction
This is the first in my series of biclustering posts. It serves as an introduction to the concept. The later posts will cover the individual algorithms that I am implementing for scikit-learn.
Before talking about biclustering, it is necessary to cover the basics of clustering. Clustering is a fundamental problem in data mining: given a set of objects, group them according to some measure of similarity. This deceptively simple concept has given rise to a wide variety of problems and the algorithms to solve them. scikit-learn provides a number of clustering methods, but these represent only a small fraction of the diversity of the field. For a more detailed overview of clustering, there are several surveys available [1, 2, 3].
In many clustering problems, each of the $n$ objects to be clustered is represented by a $p$-dimensional feature vector. The entire dataset may then be represented by a matrix of shape $n \times p$. After applying some clustering algorithm, each object belongs to one cluster. (Note: other types of clustering and biclustering methods exist that do not perform hard assignment. For examples, see hierarchical clustering and fuzzy clustering.)
To demonstrate, consider a clustering problem with 20 samples and 20 dimensions. Here is a scatterplot of the first two dimensions, with cluster membership designated by color:
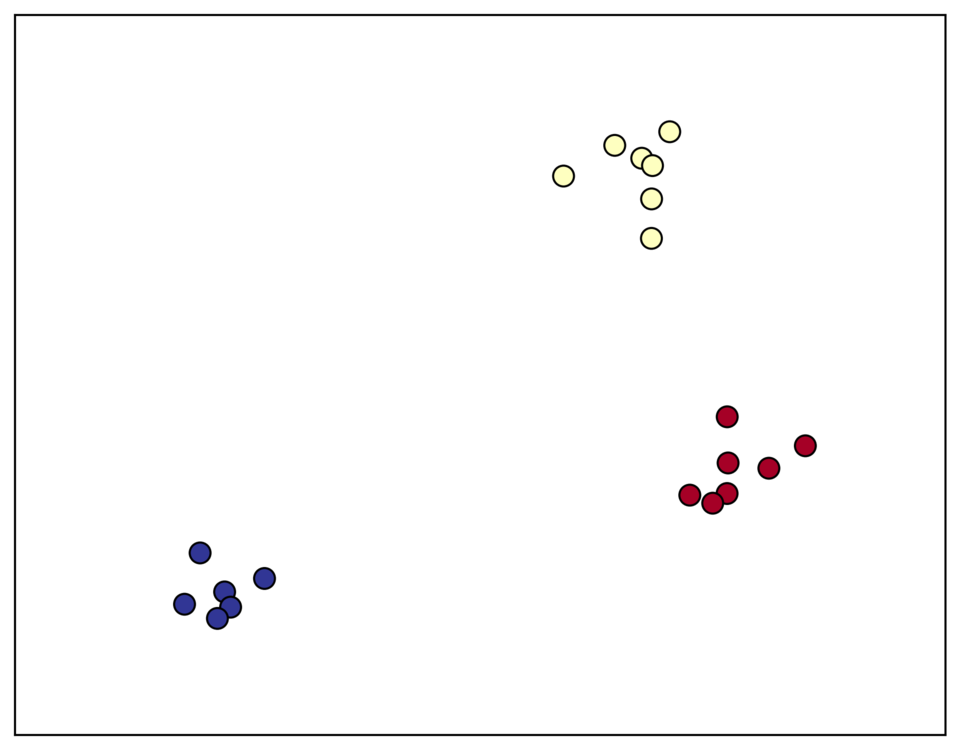
In the original design matrix the clusters are not immediately visible:

By rearranging the rows of the matrix, the samples belonging to each cluster can be made contiguous. In the rearranged matrix, the correct partition is more obvious:

This view of clustering as partitioning the rows of the data matrix can be generalized biclustering, which can be viewed as partitioning both the rows and the columns simultaneously. Clustering both rows and columns together may seem a strange and unintuitive thing to do. To see why it can be useful, let us consider a simple example.
Motivating example: throwing a party
Bob is planning a housewarming party for his new three-room house. Each room has a separate sound system, so he wants to play different music in each room. As a conscientious host, Bob wants everyone to enjoy the music. Therefore, he needs to distribute albums and guests to each room in order to ensure that each guest hears their favorite songs.
Our host has invited fifty guests, and he owns thirty albums. He sends out a survey to each guest asking if they like or dislike each album. After receiving their responses, he collects the data into a $50 \times 30$ binary matrix $\boldsymbol M$, where $M_{ij}=1$ if guest $i$ likes album $j$.
In addition to ensuring everyone is happy with the music, Bob wants to distribute people and albums evenly among the rooms of his house. All the guests will not fit in one room, and there should be enough albums in each room to avoid repetitions. Therefore, Bob decides to bicluster his data to maximize the following objective function:
$$s(\boldsymbol M, \boldsymbol r, \boldsymbol c) = b(\boldsymbol r, \boldsymbol c) \cdot \sum_{i, j, k} M_{ij} r_{ki} c_{kj}$$
where $r_{ki}$ is an indicator variable for membership of guest $i$ in cluster $k$, $c_{kj}$ is an indicator variable for album membership, and $b \in [0, 1]$ penalizes unbalanced solutions, i.e., those with biclusters of different sizes. As the difference in sizes between the largest and the smallest bicluster grows, $b$ decays as:
$$b(\boldsymbol r, \boldsymbol c) = \exp \left ( \frac{ - \left ( \max \left ( \mathcal S \right ) - \min \left ( \mathcal S \right ) \right )}{ \epsilon } \right )$$
where
$$\mathcal S = \left \{ \left (\sum_{i} r_{ki} \right ) \cdot \left (\sum_{j} c_{kj} \right ) | k = 1..3 \right \}$$
is the set of bicluster sizes, and $\epsilon > 0$ is a parameter that sets the aggressiveness of the penalty.
Bob uses the following algorithm to find his solution: starting with a random assignment of rows and columns to clusters, he reassigns row and columns to improve the objective function until convergence. In a simulated annealing fashion, he allows suboptimal reassignments to avoid local minima. However, this algorithm is not guaranteed to be optimal. Had Bob wanted the best solution, the naive approach would require trying every possible clustering, resulting in $k^{n+p} = 3^{80}$ candidate solutions. This suggests that Bob’s problem is in a nonpolynomial complexity class. In fact, most formulations of biclustering problems are in NP-complete [5].
Here is the matrix for the original data set:

After biclustering, the rows and columns of the data matrix may be reordered to show the assignment of guests and albums to rooms:

Although not everyone will enjoy every album, this solution ensures that most guests will enjoy most albums.
Conclusion
This article introduced biclustering through a contrived example, but these methods is not limited to throwing great parties. Any data that can be represented as a matrix is amenable to biclustering. It is a popular technique for analyzing gene expression data from microarray experiments. It has also been applied to recommendation systems, market research, databases, financial data, and agricultural data, as well as many other problems.
These diverse problems require more sophisticated algorithms than Bob’s party planning algorithm. His algorithm only works for binary data and assigns each row and each column to exactly one cluster. However, many other types of bicluster structures have been proposed. Those interested in a more detailed overview of the field may be interested in the surveys [4, 5, 6].
In the following weeks I will introduce some popular biclustering algorithms as I implement them. The next posts will cover spectral biclustering.
References
[1] Jain, A. K., Murty, M. N., & Flynn, P. J. (1999). Data clustering: a review. ACM computing surveys (CSUR), 31(3), 264-323.
[2] Berkhin, P. (2006). A survey of clustering data mining techniques. In Grouping multidimensional data (pp. 25-71). Springer Berlin Heidelberg.
[3] Jain, A. K. (2010). Data clustering: 50 years beyond K-means. Pattern Recognition Letters, 31(8), 651-666.
[4] Tanay, A., Sharan, R., & Shamir, R. (2005). Biclustering algorithms: A survey. Handbook of computational molecular biology, 9, 26-1.
[5] Madeira, S. C., & Oliveira, A. L. (2004). Biclustering algorithms for biological data analysis: a survey. Computational Biology and Bioinformatics, IEEE/ACM Transactions on, 1(1), 24-45.
[6] Busygin, S., Prokopyev, O., & Pardalos, P. M. (2008). Biclustering in data mining. Computers & Operations Research, 35(9), 2964-2987.